Речь пойдет о значимых числах в истории человечества. Начнем, пожалуй, с числа Эйлера, или как многие его знают: число е.
Откуда оно взялось? Для этого нужно обратиться к истории. В 17 веке Якоб Бернулли занялся решением задачи о сложных процентах. Что же это за задача?
Представьте, что вы положили под процент 100 рублей в очень щедрый банк, который готов вам выплачивать 100% годовых. То есть, через год вы получите еще 100 рублей и в итоге вы будете иметь 200. И вдруг банк предлагает вам получать по 50% каждые пол года. Согласитесь ли вы? Давайте посчитаем: после первых полгода вы получите 50 рублей, что в итоге выльется в 150 рублей в вашем распоряжении. Еще через полгода вы снова получите 50%, но уже от 150, то есть еще 75 рублей. Таким образом, через год вы будете иметь 225 рублей!
Несомненно, нужно соглашаться! Давайте пойдем дальше: что если мы будем получать по 25% каждый квартал? Тогда сумма на вашем счету в конце года составит около 244-х рублей!(если хотите можете посчитать сами)
А каждый месяц? Чтобы не заниматься долгими вычислениями, давайте выведем формулу. Чтобы узнать, сколько будет на вашем счету в конце месяца, вам нужно: изначальную сумму умножить на 1+1/12. Если же мы хотим узнать сумму, которая будет в конце года, то эту (1+1/12) нужно возвести в 12 степень.

Таким образом, мы получим 261 рубль в конце года.
Тут можно сделать вывод, что чем чаще мы получаем доход, тем больше денег получим. Давайте попробуем получить формулу для произвольного количества операций. Видна следующая закономерность:

Где n - число получения прибыли в год. Если мы хотим узнать, какой будет максимальная прибыль, мы должны получать прибыть постоянно, непрерывно. Для этого число n нужно устремить к бесконечности.
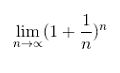
И здесь мы получили удивительное выражение, которое называется вторым замечательным пределом.
Бернулли не смог найти формулу для отыскания численного значения этого предела. Это удалось сделать только через 50 лет. Леонард Эйлер или Карл Гаусс, до сих пор не известно кто сделал это первым. Эйлер доказал, что это число иррациональное. Он нашел несколько формул для вычисления этого предела, и число, к которому он стремится он назвал числом е.
Почему е так важна? Потому что это язык естественного роста чего-либо. В любой точке графика функции e^x значение производной (градиента) будет равняться е^x . Кроме того, площадь под графиком этой функции всегда будет равна e^x. Таким образом значение функции, ее производной и площади под графиком всегда совпадают! Это единственная и уникальная функция такого рода, она встречается во многих отраслях жизни и науки человека. В экономике, физике, демографии и так далее.





